Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 80
Duas barras são interligadas por uma ligação curta BC. Determine as componentes da reação no apoio fixo A e no pino D.
Passo 1
Começamos desenhando o diagrama do corpo livre dos trechos AB e BD:
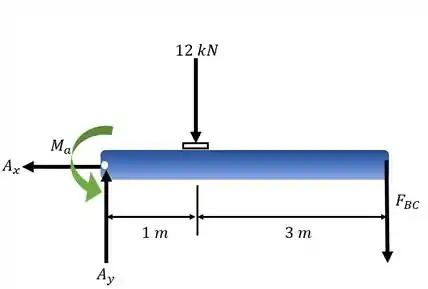
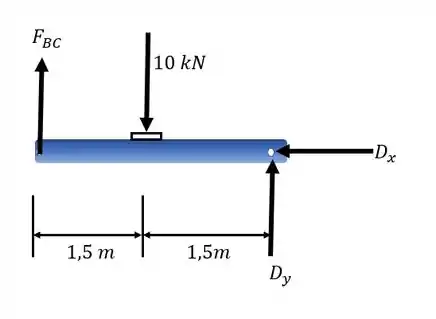
Passo 2
Podemos começar escrevendo a equação equilíbrio em relação ao momento no ponto D:
Passo 3
Podemos escrever a equação do equilíbrio no eixo x:
Passo 4
Podemos escrever a equação do equilíbrio para o momento em relação ao ponto B:
Passo 5
Agora, considerando o diagrama do membro AC, podemos usar a equação do equilíbrio no eixo x:
Passo 6
Analogamente para o eixo y:
Passo 7
Por fim, podemos utilizar a equação do equilíbrio em relação ao momento para o ponto A:
Resposta
Exercícios de Livros Relacionados
Um contrapeso de 300 k g , com centro de massa em G , é montado na manivela A B da unidade de bombeamento de petróleo. Se uma força F = 5 k N deve ser desenvolvida no cabo fixo conectado à extremidade
O cortador de tudo é preso em volta do tubo P . Se a roda em A exerce uma força normal F a = 80 N sobre o tubo, determine as forças normais das rodas B e C sobre o tubo. As três rodas possuem um raio
A estrutura de dois membros é conectada em C por um pino, que está fixado em B D E e atravessa o rasgo no membro A C . Determine as componentes horizontal e vertical da reação nos apoios.
A estrutura é usada para sustentar o cilindro de 50 k g . Determine as componentes horizontal e vertical da reação em A e D .
3.23. Determine o comprimento não deformado da mola AC se uma força P = 400N torna o ângulo θ = 60 ° para o equilíbrio. A corda AB tem 0,6m de extensão. Considere k = 850 N m .