Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 63
Determine o produto de inércia para a área em relação aos eixos e .
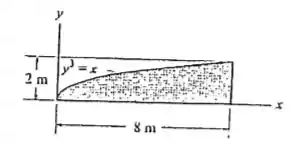
Passo 1
Como o enunciado foi bem direto com relação ao que deseja, então, vamos direto ao ponto. Tomemos, primeiramente as coordenadas do centroide da figura
Nosso diferencial de área é dado por , dessa forma vamos ter
Nosso produto de inércia, vai ser a integral de ambos os lados. Dessa forma, temos