Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 67
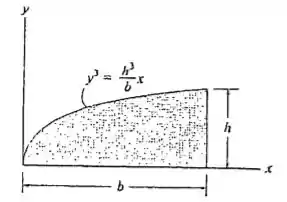
Determine o produto de inércia para a área em relação aos eixos e .
Passo 1
Cara, para calcular o produto de inércia dessa figura, vamos ter que calcular uma integralzinha. Mas tem um passo a passo para montar ela. Vem que vai dar bom!
Vamos começar pegando um retângulo bem fininho paralelo a (com espessura ), contido na nossa área. O chamamos de elemento diferencial. Na nossa figura que será dado por
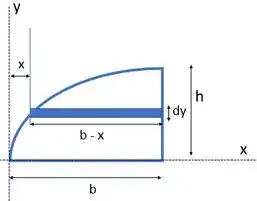
Percebe que a largura dele é , então a área dele é dada por:
Guarda isso, que a gente vai precisar. Vamos seguir!
Passo 2
O produto de inércia desse elemento diferencial em relação aos eixos pode ser determinado usando o teorema dos eixos paralelos para o produto de inércia
Onde representam a localização do centroide do nosso elemento.
Como temos um retângulo, uma figura simétrica, o termo zera. Sendo assim, vamos substituir os dados que já temos na equação acima, de tal modo que obteremos
Passo 3
Precisamos achar esses e . O centroide do retângulo é no centro dele. Vamos ver as coordenadas desse centro na figura:
Daí
E nosso produto de inércia fica:
Mas como a gente tem um , precisamos que tudo esteja em função de . Da equação dada na imagem temos que
Assim, substituindo em vamos encontrar
Passo 4
Pronto, agora basta integrarmos de até a altura da nossa figura que é , que é o intervalo onde nossa área está em relação a , assim, vamos obter como resultado
Onde, finalmente, chegamos em
E está resolvido o nosso problema.