Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 66
Determine o produto de inércia para a área em relação aos eixos e .
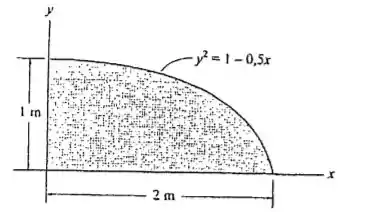
Passo 1
Queremos encontrar o produto de inércia e para isso tomemos as coordenadas do centroide e o diferencial de área
Sendo assim, nosso diferencial do produto de inércia vai ser dado por
Integrando ambos os lados, vamos obter