Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 1
Determine a massa e a localização do centro de massa da barra em formato parabólico uniforme. A massa por unidade de comprimento da barra é .
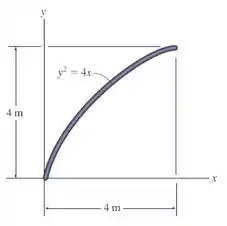
Passo 1
Seja um diferencial de comprimento que vamos destacar nessa barra em formato parabólico aqui.
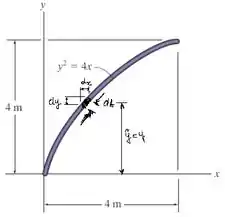
Podemos escrever da seguinte maneira:
Mas quem é ? Podemos escontrar esse valor a partir da equação que define o formato do arco! Sabemos que . Vamos isolar a variável e derivar em relação a .
Tenso esse resultado em mãos, vamos substituí-lo na equação de :
Passo 2
O elemento de massa pode ser expresso da seguinte maneira:
Como já encontramos o diferencial de massa do objeto, podemos calcular a integral dele e achar o valor da massa ! Assim,
Passo 3
O centroide do elemento representar o centro geométrico de um corpo, que coindice com o centro de massa ou centreo de gravidade se o maetrial que compõe for o corpo uniforme ou homogêneo. Assim, o centroide desse corpo está localizado em e .
Vamos encontrar agora o valor para .
Resposta
O valor da massa é:
O centroide é igual a: