Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 74

Determine o produto de inércia para a área da seção transversal em relação aos eixos x e y, que têm sua origem localizada no centroide C.

Passo 1

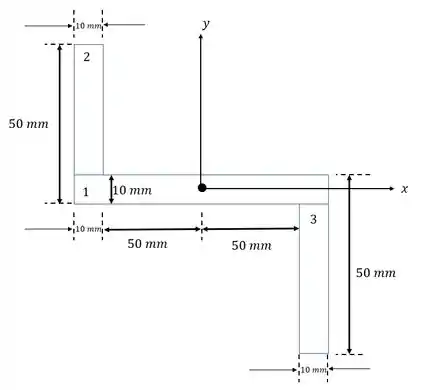
Passo 2

Podemos começar calculando a área dos retângulos 1,2,3:

A 1 = 120 × 10 = 1200   m m 2 A 2 = 40 × 10 = 400   m m 2 A 3 = 40 × 10 = 400   m m 2

Passo 3

Dada a simetria, I x y - 1 , I x y - 2   e   I x y - 3   =   0

Passo 4

O retângulo 1 é simétrico ao eixo x, portanto seu produto de inércia é zero:

I x y 1 = 0

Passo 5

Calculando o produto de inércia do retângulo 2:

I x y 2 = I x y - 2 + A 2 d x d y

Da simetria, I x y - 2 = 0

I x y 2 = 0 + 40 × 10 × - 55 × 25 I x y 2 = - 0,55 × 10 6   m m 4

Passo 6

Calculando o produto de inércia do retângulo 3: I x y 3 = I x y - 3 + A 3 d x d y I x y 3 = 0 + 40 × 10 × 55 × - 25 I x y 3 = - 0,55 × 10 6   m m 4

Passo 7

O produto de inércia da peça portanto, é

I x y = I x y 1 + I x y 2 + I x y 3 I x y =   0 + - 0,55 × 10 6 - 0,55 × 10 6 I x y = - 1,1 × 10 6   m m 4

Resposta

I x y = - 1,1 × 10 6   m m 4

Ver Outros Exercícios desse livro