Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas fundamentais - Ex. 7
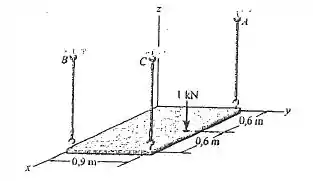
A chapa uniforme tem um peso de . Determine a tração em cada um dos cabos que a sustentam.
Passo 1
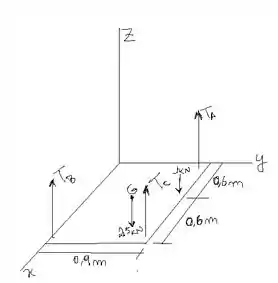
Em toda questão de mecânica geral nós sempre devemos desenhar o diagrama de corpo livre da situação para entendermos quais são as forças e componentes envolvidas. Temos nessa situação as trações das cordas , o peso da chapa no centro dela () e uma força aplicada na placa de .
Passo 2
Sabemos que em todo sistema em equilíbrio, a soma das forças horizontais e verticais é zero. Na nossa questão, as forças e tensões não possuem componentes horizontais, todas estão perpendiculares à chapa. Assim, só nos resta a soma das forças verticais:
Passo 3
Vamos agora calcular o momento em relação ao eixo . Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:
Passo 4
Vamos também olhar o momento em relação ao eixo . Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:
Passo 5
Temos agora três equações e três icógnitas. Basta resolver o resistema para encontrarmos os valores das tensões!
Vamos substrair a primeira e a segunda equação. Isso nos dá:
Vamos substituir o valor de na terceira equação.
Por fim, vamos substituir o valor de e na primeira equação do sistema
Resposta
Os valores para as trações são: