Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 72

Determine o produto de inércia para a área da seção transversal da viga em relação aos eixos x e y que têm sua origem localizada no centroide C.

Passo 1

Desenho:

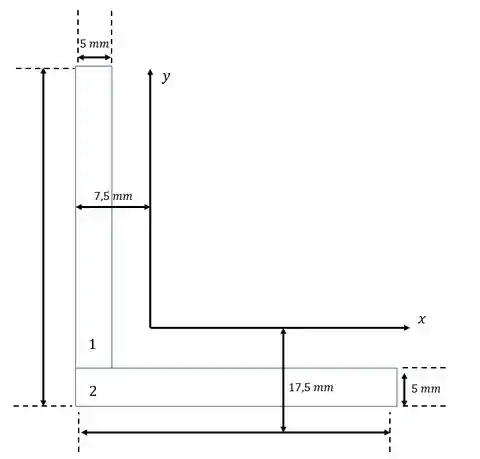
Passo 2

Calculando as áreas dos retângulos 1 e 2: A 1 = 30 × 5 = 150   m m 2 A 2 = 45 × 5 = 225   m m ²

Passo 3

Da expressão, podemos calcular diretamente o produto de inércia do retângulo 1: I x y 1 = I x y 2 - + A 1 d x d y Nesse caso, I x y 2 - = 0

I x y 1 = 0 + 150 × 30 2 - 7,5 - 17,5 + 5 2 I = - 16875   m m 4

Passo 4

Analogamente, podemos calcular diretamente o produto de inércia do retângulo 2:

I x y 2 = I x y 2 - + A 2 d x d y

Nesse caso, I x y 2 - = 0

I x y 2 = 0 + 225 × - 7,5 + 5 2 45 2 - 12,5

I x y 2 = - 11250 m m 4

Passo 5

O produto de inércia da peça é:

I x y = I x y 1 + I x y 2 = - 16875 - 11250 I x y = - 28,125   m m 4

Resposta

I x y = - 28,125   m m 4

Ver Outros Exercícios desse livro