Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 174
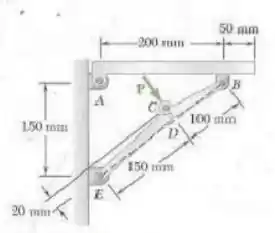
Uma prateleira de é mantida na horizontal por uma mão francesa dobrável que consiste em duas partes e articuladas em e apoiadas um contra a outra em . Determine a força necessária para se soltar esse suporte.
Passo 1
Primeiramente vamos calcular o peso da nossa estante que é dado por
Aplicando as condições de equilíbrio para um corpo na estante vamos ter
Passo 2
Agora, analisaremos e utilizando as condições de equilíbrio vamos ter
Tomando para análise teremos
Por fim, para encontrarmos o que desejamos vamos substituir em obtendo assim
E pronto, está resolvido nosso problema.
Resposta
Exercícios de Livros Relacionados
Determine o maior peso P 2 que pode ser aplicado à trelila de modo que a força em qualquer membro não exceda 2,5k N (T) ou 1,75k N (C). Considere P 1 = 0 .
Determine a força em cada membro da treliça e diga se os membros estão sob tração ou compressão. Faça P 1 = 1200N e P 2 = 500k N .
Remova as forças de 6k N e determine a maior força P que pode ser aplicada à treliça de modo que nenhum dos membros esteja sujeito a uma força que exceda 10k N em tração ou 7,5k N em compressão.
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. Faça P = 5k N
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.