Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 10

Determine os produtos de inércia I x y ,   I y z   e   I x z do sólido homogêneo. O material tem uma densidade de 7,85   M g / m 3 .

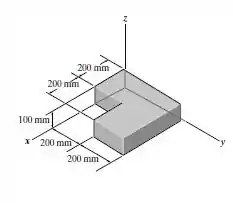
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom, a estratégia para resolver produtos de inércia é dividir o desenho de uma forma que nos ajude. E calcular os produtos de cada um separadamente.

Vamos calcular o produto de Inércia do sólido completo ( 1 ) e do sólido como a parte que está faltando ( 2 ) . O produto de inércia da nossa figura será a subtração dos dois:

As massas são dadas por:

m 1 = ρ V 1

m 1 = 7850 0,4 0,4 0,1

m 1 = 125,6   k g

m 2 = ρ V 2

m 2 = 7850 0,2 0,2 0,1

m 2 = 31,4   k g

Os produtos de inércia são dados por:

I x y = ∑ ( T x ' y ' + m x G y G )

I y z = ∑ ( T y ' z ' + m y G z G )

I x z = ∑ ( T x ' z ' + m x G z G )

Por simetria sabemos que tanto pra o sólido 1 , como para o sólido 2 ,   T x ' y ' = T y ' z ' = T x ' z ' = 0 , portanto:

I x y = 0 + 125,6 ( 0,2 ) ( 0,2 ) - 0 + 31,4 ( 0,3 ) ( 0,1 )

I x y = 4,08   k g ⋅ m 2

I y z = 0 + 125,6 ( 0,2 ) ( 0 , 05 ) - 0 + 31,4 ( 0 , 1 ) ( 0,05 )

I y z = 1,10   k g ⋅ m 2

I x z = 0 + 125,6 ( 0,2 ) ( 0,05 ) - 0 + 31,4 ( 0,3 ) ( 0,05 )

I x z = 0,785   k g ⋅ m 2

Resposta

I x y = 4,08   k g ⋅ m 2

I y z = 1,10   k g ⋅ m 2

I x z = 0,785   k g ⋅ m 2

Ver Outros Exercícios desse livro