Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 18
Determine a força constante que deve ser aplicada à corda a fim de fazer com que o bloco A de 15 kg tenha uma velocidade de quando for deslocado para cima partindo do repouso. Despreze o peso das polias e da corda.
Passo 1
Esta é uma questão bem simples. Um jogo de polias. Precisamos descobrir a força atuante em A responsável por causar uma velocidade de no corpo após o mesmo subir . Vamos trabalhar inicialmente com as polias, uma por vez, a fim de obter a aceleração em função da força F. Posteriormente, será necessário utilizar as equações da cinemática para resolver obtermos a força.
Passo 2
Vamos começar a ver a atuação das forças na polia C inicialmente. Esquematicamente, temos:
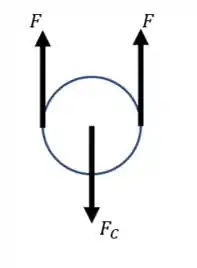
Por se tratar de uma corda, as duas forças para cima são iguais entre si (cada força atuando sobre cada “trecho” da corda). Para contrabalancear essas forças, surge uma força . Como a polia está em um movimento constante, temos:
Fazendo a mesma análise para a polia A, temos:
Novamente, como a polia está em equilíbrio, temos:
Passo 3
Agora que descobrimos a força para baixo em A, devido a terceira lei de Newton (Ação e Reação), teremos esta mesma força atuando para cima no corpo A. Este corpo possui o seguinte diagrama de forças.
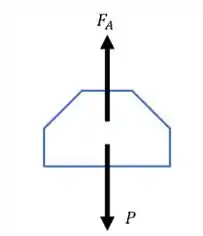
Em que é o peso do corpo. Portanto, para descobrirmos a aceleração à qual o corpo está sujeito, basta aplicarmos a lei de Newton. Sendo assim,
Agora que descobrimos a aceleração em função da força F, basta descobrirmos qual a aceleração que causa a velocidade dada.
Passo 4
Agora, só nos basta utilizarmos as leis da cinemática. Como a aceleração é constante, temos: