Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 8.Problemas - Ex. 8

Determine a solução de vibração livre de uma corda fixa em ambas as extremidades quando suas condições iniciais são dadas por...

w x , 0 = 0 ,     ∂ w ∂ t x , 0 = 2 a x l   p a r a   0 ≤ x ≤ l 2

E

∂ w ∂ t x , 0 = 2 a 1 - x l   p a r a   l 2 ≤ x ≤ l

Passo 1

E aí, galerinha!

Bom! Bora lá pro que interessa!

Antes de mais nada, vamo pra uma introduçãozinha!

Pra corda fixa em ambas as extremidades, como mostrado na figura abaixo...

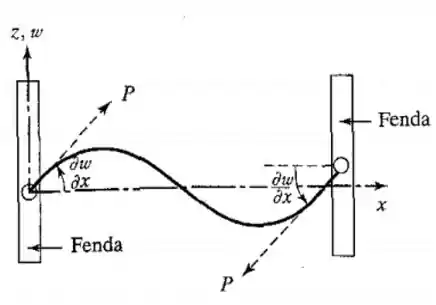
E outra coisa que a gente sabe da nossa bibliografia, é que a solução geral nas condições de contorno dadas por...

W 0 = 0

W l = 0

É igual à...

W x , t = ∑ n = 1 ∞ W n ( x , t )

W x , t = ∑ n = 1 ∞ sen ⁡ n π x l C n cos ⁡ n c π t l + D n sen ⁡ n c π t l

Onde...

C n = 2 l ∫ 0 l W 0 x sen ⁡ n π x l d x

D n = 2 n c π ∫ 0 l W ˙ 0 x sen ⁡ n π x l d x

Passo 2

Pois muito bem! Já sabemos que uma das condições de contorno é...

W 0 = W x , 0 = 0

Logo, substituindo na fórmula, obtemos que...

W x , 0 = ∑ n = 1 ∞ sen ⁡ n π x l C n cos ⁡ n c π 0 l + D n sen ⁡ n c π 0 l = 0

∑ n = 1 ∞ sen ⁡ n π x l C n = 0

A maior possibilidade disso aí dar zero é quando...

C n = 0

Ficamos então, com...

W x , t = ∑ n = 1 ∞ sen ⁡ n π x l D n sen ⁡ n c π t l

Passo 3

Vamos então, obter D n !

Bom! W 0 ( x ) é dado por...

W 0 x = 2 a x l     p a r a   0 ≤ x ≤ l 2 2 a ( l - x ) l     p a r a   l 2 ≤ x ≤ l

Dessa forma, ficamos com...

D n = 2 n c π ∫ 0 l 2 2 a x l sen ⁡ n π x l d x + ∫ l 2 l 2 a 1 - x l sen ⁡ n π x l d x

D n = 2 n c π 2 a - 1 π n x cos ⁡ n π x l + l π 2 n 2 sen ⁡ n π x l 0 l 2 + a - 2 l π n cos ⁡ n π x l + 2 a x π n cos ⁡ n π x l - l a 2 π 2 n 2 sen ⁡ n π x l l 2 l

D n = 8 a l π 3 c n 3 sen ⁡ n π 2

Bom! Acontece que como estamos trabalhando com série, tá ligado que para determinado valor de n , aquele sen ⁡ n π 2 ora vai ser igual à 0 ; ora vai ser igual à 1 ou - 1 .

Podemos então, escrever ele como...

D n = 0 ,     s e   n   é   p a r 8 a l π 3 c n 3 - 1 n - 1 2 ,     s e   n   é   i m p a r

Dessa forma, substituindo esse D n na expressão do W ( x , t ) :

W x , t = ∑ n = 1 ∞ sen ⁡ n π x l D n sen ⁡ n c π t l

E fazendo uns ajuste no somatório, já que D n só assume valor não nulo quando n é impar

W x , t = ∑ n = 1,3 , 5 , … ∞ 8 a l π 3 c n 3 - 1 n - 1 2 ⋅ sen ⁡ n π x l ⋅ sen ⁡ n c π t l

Pronto! Achamos nossa resposta!

Resposta

W x , t = ∑ n = 1,3 , 5 , … ∞ 8 a l π 3 c n 3 - 1 n - 1 2 ⋅ sen ⁡ n π x l ⋅ sen ⁡ n c π t l

Ver Outros Exercícios desse livro