Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 91
Determine a tensão normal máxima desenvolvida na barra quando sujeita a uma carga .
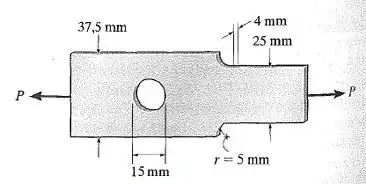
Passo 1
Uma barra é esticada por uma tração . Queremos saber a tensão normal máxima!
A fórmula da tensão normal média é
A tensão será maior nas regiões que tem menor área transversal!
Mas além disso, temos duas regiões que trazem complicações: a barra possui um furo e variação rápida de área transversal (filete de rebaixo). Essas regiões irão concentrar tensões!
A tensão máxima certamente ocorre em uma dessas duas regiões. Precisamos checar as tensões nessas duas regiões e ver qual é maior!
Pra começar, vamos reunir tudo que sabemos da barra.
Características da barra:
- Largura maior: .
- Largura menor: .
- Raio do filete:
- Raio do furo: .
- Espessura:
Essa é a parte mais importante nesse tipo de questão, porque é o que vamos precisar pros gráficos de concentração de tensão.
A tensão máxima é encontrada a partir da tensão média :
Precisamos encontrar o em cada caso: o fator de concentração de tensão!
Passo 2
Vamos ver primeiro para o filete.
Queremos achar o para filete de rebaixo. O gráfico para isso é a figura 4.24 e precisa das seguintes quantidades:
Checando o gráfico, temos aproximadamente que 73
Show! Agora calculamos a tensão média, segundo o gráfico nos indica:
Repara que nossa área é a área transversal da seção referente ao filete, onde há um estreitamento da barra.
E finalmente, a tensão máxima:
Passo 3
Agora vamos checar o furo!
Queremos achar o para o furo. O gráfico para isso é a Figura 4.25 e precisa das seguintes quantidades:
Checando o gráfico, temos .
Vamos para a tensão média. Confira o gráfico para calcular como ele pede:
Repara que a área aqui é a área da seção vertical que passa pelo meio do furo.
E finalmente, a tensão máxima:
Passo 4
Comparando, . Então a tensão máxima na barra inteira é
Resposta
Tensão máxima: .