Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 94
Determine o volume gerado girando a área semicircular em 180 ∘.
Passo 1
Usando o teorema de Pappus, podemos escrever a expressão para o volume do corpo como
Onde x ‾ é o centroide da área, A é a área e o ângulo de rotação θ
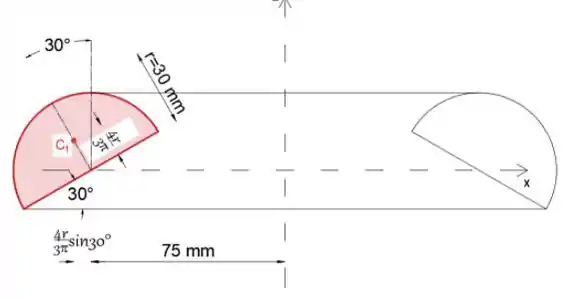
Obtivemos na Tabela que a distância entre o centróide do semicírculo até sua base é 4r / 3π, então, como o raio do círculo é r = 30 mm, a distância entre seu centróide e o eixo z é:
Uma vez que meia área do círculo é
O ângulo de rotação
Passo 2
Coloque todos os valores na expressão (2)
O volume total é
Resposta
Exercícios de Livros Relacionados
Um furo com raio r deve ser feito no centro do bloco homogêneo. Determine a profundidade h do furo de modo que o centro de gravidade G seja o mais baixo possível.
Determine a profundidade h do furo de 100m m de diâmetro feito na base do cone de modo que o centro de massa do sólido resultante esteja localizado em z -=115m m . O material tem densidade de 8M g / m
A placa composta é feita de segmentos de aço ( A ) e latão ( B ) . Determine a massa e a localização ( x - ,y - ,z - ) de seu centro de massa G . Considere ρ a ç o = 7,85M g / m 3 ç e ρ l a t ã o = 8,
Determine a distância z - até o centroide do sólido que consiste em um cone com um furo de altura h=50m m feito em sua base.
Determine a localização y do centroide C da viga com a seção transversal mostrada.