Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 54
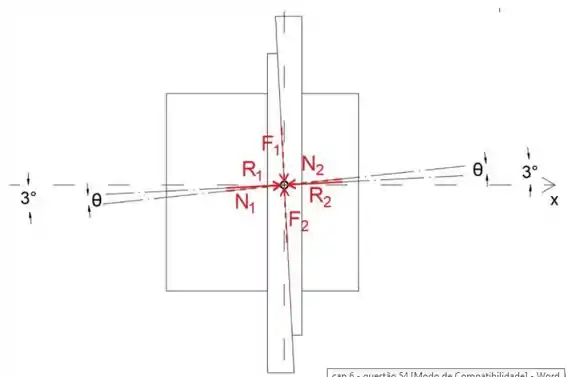
Na construção de estrutura de madeira, dois calços são freqüentemente usados para preencher a lacuna entre a moldura S e a janela / batente da porta mais fina D. Os membros S e D são mostrados em seção transversal na figura. Para os 3 ^ ∘ calços mostrados, determine o coeficiente mínimo de atrito estático necessário para que os calços permaneçam no lugar.
Passo 1
Olhando para o diagrama de corpo livre, podemos notar que as forças normais e de fricção são iguais para ambos os calços
Uma vez que precisamos encontrar coeficiente mínimo de atrito, as forças de atrito devem ser forças de atrito máximas
Passo 2
T ambém podemos notar que a soma de dois ângulos θ é 3 ∘, portanto
Uma vez que determinamos o ângulo θ, podemos calcular o valor para a força de atrito mínima