Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 135
Detrmine a equação da curva da linha elástica para a viga. Especifique a inclinação e o deslocamento em A. EI é constante.
Passo 1
Fala aí pessoal, partiu mais um problema de resmat!
Este problema pede as reações de apoio. Como é uma viga mais simples, vamos economizar seu tempo e ir direto para o DCL:
Aí a gente acha a valor do momento na nossa viga em função de . Vamos cortar ela e olhar só para a direita. Mas repara que quando a gente corta, a altura do triângulo vai depender de ? Então a gente precisa achar uma expressão para ela:
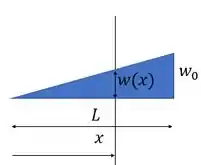
Aí o momento fica
Bora seguir!
Passo 2
Sabemos que a equação da linha elástica e sua inclinação podem ser obtidas determinando o momento interno no elemento em função de .
Neste caso, temos várias cargas agindo e, por isso, devemos integrar . Ao integrar uma vez, otemos a equação para a inclinação da linha elástica, e integrando novamente, obtemos a equação para a deflexão. Temos:
Passo 3
Com isso, temos as condições de contorno. São elas:
Ou seja, no apoio do engaste, e inclinação zeram.
Substituindo as condições de contorno na equação, temos:
Assim, nossa equação da linha elástica vai ser:
E a inclinação:
Passo 4
Por fim, a inclinação em ocorre em . Sendo assim:
E o deslocamento, também ocorre em . Por isso: