Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 34

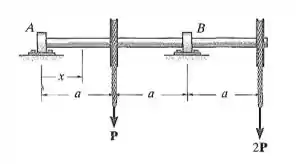
O eixo suporta as cargas das duas polias mostradas na figura. Determine a equação da linha elástica. Os mancais em A e B exercem somente reações verticais sobre o eixo. EI é constante.

Passo 1

Primeiramente, vamos determinar as reações de apoio:

∑ M a = 0 → - P a + 2 a V b - 2 P × 3 a = 0

V b = 7 P 2

∑ F y = 0 → - V a + V b - P - 2 P = 0

V a = P 2

Logo, montando a equação do momento, ficaremos com:

M x = - P 2 < x - 0 >   - P < x - a > + 7 P 2 < x - 2 a >

Passo 2

Sabemos que:

E I d 2 v d x 2 = M x = - P 2 < x - 0 >   - P < x - a > + 7 P 2 < x - 2 a >

Integrando-se os dois lados 2 vezes, temos:

E I v = - P 12 x 3 - P 6 < x - a > 3 + 7 P 12 < x - 2 a > 3 + C 1 x + C 2

As condições de contorno são:

x = 0 → v = 0

x = 2 a → v = 0

Logo, temos:

C 1 = 5 P a 2 12 ; C 2 = 0

A equação da linha elástica será:

v = P 12 E I - x 3 - 2 < x - a > 3 + 7 < x - 2 a > 3 + 5 a 2 x  

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Detrmine a equação da curva da linha elástica para a viga. Especifique a inclinação e o deslocamento em A. EI é constante.