Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 30

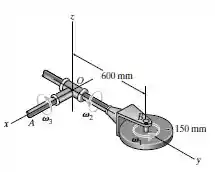
O disco circular de 10   k g gira em torno de seu eixo com uma velocidade angular constante ω 1 = 15   r a d / s . Simultaneamente, o braço O B e o eixo O A giram em torno dos seus eixos com velocidades angulares constantes ω 2 = 1 0   r a d / s e ω 3 = 6   r a d / s , respectivamente. Determine a quantidade de movimento angular do disco em relação ao ponto O e sua energia cinética.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos imaginar um novo sistema de coordenadas que passa no centro do disco de 150   m m , ( x ' , y ' , z ' ) como mostrado na figura abaixo:

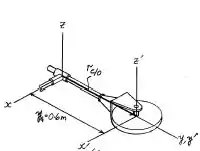
Os momentos de inercia do disco com relação ao centroide são dados por:

I x ' = I y ' = 1 4 m r 2

I x ' = I y ' = 1 4 10 0,15 2

I x ' = I y ' = 0,05625   k g ⋅ m 2

I z ' = 1 2 m r 2  

I z ' = 1 2 ( 10 ) ( 0,15 ) 2

I z ' = 0,1125   k g ⋅ m 2

Por simetria sabemos que I x ' y ' = I y ' z ' = I x ' z ' = 0 .

O vetor velocidade angular resultante, é dado pela soma das velocidades angulares ω 1 e ω 3 . Temos:

ω = ω 1 + ω 2 + ω 3

ω = 6 i + 10 j + 15 k

Podemos calcular o momento angular do disco com relação ao centro de massa aplicando:

H x = I x ' ω x

H x = 0,05625 ( 6 )

H x = 0,3375   k g ⋅ m 2 / s

H y = I y ' ω y

H y = 0,05625 ( 10 )

H y = 0 , 5625   k g ⋅ m 2 / s

H z = I z ' ω z

H z = 0,1125 ( 15 )

H z = 1,6875   k g ⋅ m 2 / s

Logo:

H G = 0,3375 i + 0,5625 j + 1,6875 k   k g ⋅ m 2 / s

A velocidade escalar com relação ao centro de massa é dada por:

v G = ω 3 × r C / O

v G = ( 6 i ) × ( 0,6 j )

v G = ( 3,6 k )   m / s

Finalmente, temos todos os dados necessários para calcular a quantidade de movimento angular com relação a O :

H O = r C / D × m v G + H G

H O = ( 0,6 j ) × 10 ( 3,6 k ) + 0,3375 i + 0,5625 j + 1,6875 k

H O = 21,9375 i + 0 , 5625 j + 1 , 6875 k   k g ⋅ m 2 / s

A parcela cinética será:

T = 1 2 ω ⋅ H O

T = 1 2 15 k + 6 i ⋅ 21,9375 i + 0 , 5625 j + 1 , 6875 k

T = 81,3   J

Resposta

H O = 21,9375 i + 0 , 5625 j + 1 , 6875 k   k g ⋅ m 2 / s

T = 81,3   J

Ver Outros Exercícios desse livro