O disco, tendo uma massa de , está montado excentricamente sobre o eixo . Se o eixo está girando a uma taxa de , determine as reações nos mancais de apoio quando o disco está na posição mostrada.
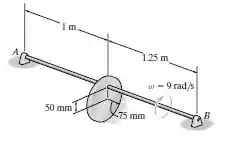
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos que:
Temos a seguinte expressão para o sistema:
A partir do diagrama de corpo livre abaixo, temos que:
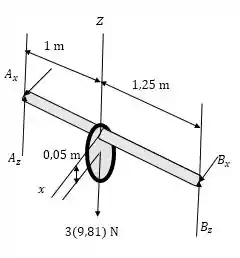
Portanto:
Analisando agora em , temos:
Analisando o somatório das forças nos eixos, temos:
Organizando as equações, temos que:
Logo:
Para as componentes em , temos: