Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 72

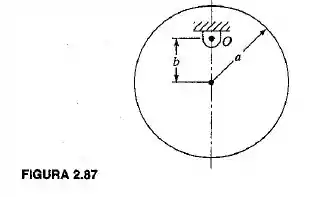
Um disco circular uniforme é articulado no ponto O , como mostra a figura 2.87 . Determine a frequência natural do sistema. Determine também a frequência máxima do sistema variando o valor de b .

Passo 1

Queremos a frequência natural do sistema dado na figura do enunciado.

Vamos calcular o momento de inércia de massa do sistema:

J O = 1 2 m a 2 + m b 2

J O = 1 2 m a 2 + 2 m b 2

A equação de movimento para o sistema fornecido é da forma:

J O θ ¨ + m g b θ = 0

Substituindo os dados conhecidos, temos que:

1 2 m a 2 + 2 m b 2 θ ¨ + m g b θ = 0

A equação generalizada de movimento para o sistema é da forma:

θ ¨ + ω n 2 θ = 0

Portanto:

θ ¨ + m g b 1 2 m a 2 + 2 m b 2 θ = 0

θ ¨ + 2 g b a 2 + 2 b 2 θ = 0

A frequência natural será:

ω n 2 = 2 g b a 2 + 2 b 2

ω n = 2 g b a 2 + 2 b 2

Passo 2

O exercício nos pede para calcular a frequência natural máxima com relação a b . Vamos derivar a função da frequência natural que encontramos no passo anterior e igualar a zero. Para encontrar os valores limites de b . Temos que:

d ω n d b = 1 2 2 g b a 2 + 2 b 2 - 1 2 a 2 + 2 b 2 2 g - 2 g b 4 b a 2 + 2 b 2 2 = 0

Resolvendo temos que:

b = ± a 2

Substituindo b = - a 2 na equação da frequência natural para encontrar seu máximo, temos que:

ω n = 2 g b a 2 + 2 b 2

ω n m á x = 2 g - a 2 a 2 + 2 - a 2 2

Desenvolvendo, temos que:

ω n m á x = g a 2

Resposta

ω n = 2 g b a 2 + 2 b 2

ω n m á x = g a 2

Ver Outros Exercícios desse livro