Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 26

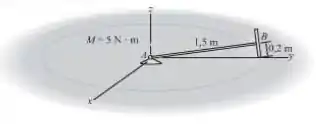
O disco de 5   k g está conectado à barra fina de 3   k g . Se a montagem está fixa a uma junta esférica em A e o momento de binário de 5   N ⋅ m é aplicado, determine a velocidade angular da barra em relação ao eixo z após a montagem ter realizado duas revoluções em torno do eixo z partinfo do repouso. O disco rola sem deslizar.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

I x = I z = 1 4 5 0,2 2 + ( 5 1,5 2 + 1 3 3 1,5 2 = 13,55

I x = 1 2 5 0,2 2 = 0,100

ω = ω y j ' + ω z k = 0,13216 ω z - ω y ' j ' + 0,99123 ω z k '

0 = 0 + 0,13216 ω z - ω y ' j ' + 0,99123 ω z k ' × 1,5 j ' + - 0,2 k '

0 = - 1,48684 ω z - 0,026433 ω z + 0,2 ω y '

ω y ' = - 7,5664 ω z

Logo:

ω = 0,13216 ω z - 7,5664 ω z j ' + 0,99123 ω z k '

ω = - 7 , 4342 ω z j ' + 0,99123 ω z k '

Para ω z = 2 r a d / s , temos:

ω = - 14,868 j ' + 1,9825 k '

Temos que:

H A = I x ' ω x i + I y ' ω y j + I z ' ω z ' k

H A = 0 + 0,1 - 14,868 j ' + 13,55 1,9825 k '

H A = - 1 , 4868 j ' + 26,862 k '

H A = - 1,4868 2 + 26,862 2

H A = 26,9   k g ⋅ m 2 / s

Resposta

H A = 26,9   k g ⋅ m 2 / s

Ver Outros Exercícios desse livro