Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 1

Mostre qua a soma dos momentos de inércia de um corpo, I x x + I y y + I z z é idependente da orientação dos eixos x, y , z e desse modo depende somente da localização da sua origem.

Passo 1

O momento de inércia para um elemento diferencial d m do corpo em relação a qualquer um dos eixos de coordenadas é definido como um produto da massa do elemento e o quadrado da distância mais curta do eixo até o elemento. Assim o momento de inércia do corpo pode ser obtida integrando-se a expressão sobre a massa total do corpo. De forma que :

I x x = ∫ m r x 2 d m = ∫ m ( y 2 + z 2 ) d m

I y y = ∫ m r y 2 d m = ∫ m ( x 2 + z 2 ) d m

I z z = ∫ m r z 2 d m = ∫ m ( x 2 + y 2 ) d m

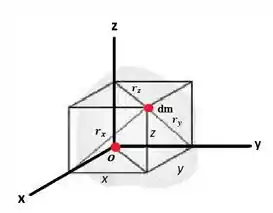
Passo 2

A soma dos momentos de inércia do corpo serão:

I x x + I y y + I z z = ∫ m ( y 2 + z 2 ) d m + ∫ m ( x 2 + z 2 ) d m + ∫ m ( x 2 + y 2 ) d m

I x x + I y y + I z z = ∫ m 2 ( x 2 +   y 2 + z 2 ) d m

Nota-se que x 2 +   y 2 + z 2 = r 2 , onde r é a distância entre a origem O e d m . Como r é constante , ele independerá da orientação dos eixos x,y e z. e portanto a soma dos momentos de inércia I x x + I y y + I z z , também independerá da orientação dos eixos, dependendo apenas da localização da sua origem.

Resposta

De acordo com os passos 1 e 2 e as considerações realizadas, foi possível provar que soma dos momentos de inércia de um corpo, I x x + I y y + I z z é idependente da orientação dos eixos x, y , z e desse modo depende somente da localização da sua origem.

Ver Outros Exercícios desse livro