Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 1
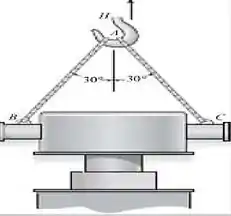
A peça fundida tem massa de Mg. Suspensa em uma posição vertical e inicialmente em repouso, recebe uma velocidade escalar de mm∕s em s utilizando o gancho do guindaste. Determine a tração nos cabos AC e AB durante este intervalo de tempo se aceleração for constante
Passo 1
Para a solução do problema primeiramente teremos que ir em busca da aceleração da peça. Sabemos inicialmente que a peça parte do repouso () e, em segundos, a peça possui uma velocidade escalar de mm∕s ou m∕s. Sabemos também que durante esse intervalo de tempo em que a peça está me movimento, sua aceleração é constante, então podemos utilizar a seguinte equação para o cálculo da aceleração da peça:
Isolando a aceleração na equação acima, temos:
Passo 2
Já temos a aceleração do bloco, agora iremos em busca da tração nos cabos que sustentam a peça, para isso, devemos obter a equação do movimento. Do diagrama de corpo livre, temos:
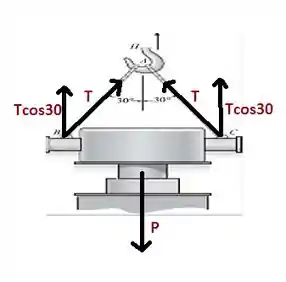
Por definição:
Assim:
Passo 3
Podemos isolar a tração na equação acima, para obter seu valor:
Substituindo os valores de na equação acima, chegaremos ao seguinte valor para a tração
kN
Resposta
A tração desenvolvida nos cabos é igual a kN