7. O dispositivo na figura é usado para desempenar a estrutura de automóveis que sofreram uma trombada. Determine a tenção de cada segmento da corrente, e , considerando que a força que o cilindro hidráulico exerce no ponto é de , como mostrado na figura.
Passo 1
Vamos considerar que a força resultante no ponto esteja em equilíbrio, então é necessário que as forças resultantes tanto na direção , quanto na direção seja zero. Logo:
Mas para fazermos isso precisamos achar o ângulo que as forças ao longo de e fazem com a horizontal e assim poder decompô-las e usar as equações acima.
Para achar esses ângulos podemos notar uma coisa, mostrado nas figuras abaixo.
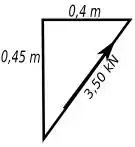
Podemos achar os angulos por uma trigonometria boba.
Na primeira figura temos:
Na segunda figura temos:
Agora temos tudo para prosseguir no problema.
Passo 2
Agora vamos abrir as equações mostradas no passo .
Passo 3
Substituindo na seguinte equação:
Poderemos encontrar . Então: