Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas Revisão - Ex. 142b
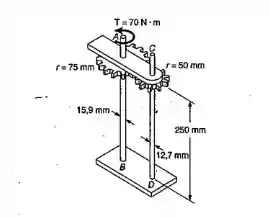
Dois eixos maciços de alumínio (G = 26 GPa) são conectados pelas engrenagens mostradas. Sabendo-se que as extremidades B e D são impedidas de girar, para o carregamento dado determinar o ângulo de torção da extremidade C.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos o eixo e dizermos qual deveria ser o ângulo para que ele tenha aquele torque ali aplicado. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser determinar a tensão e a cinemática do problema.
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
PS: esse c é o raio do nosso eixo, ok??
Resposta
Exercícios de Livros Relacionados
O eixo composto mostrado é torcido pela aplicação do torque T na extremidade A. Sabendo-se que a máxima tensão de cisalhamento na camisa de alumínio é de 60 MPa e que G = 77GPa, para o aço, e G = 26 G
Dois eixos maciços de alumínio (G = 26 GPa) são conectados pelas engrenagens mostradas. Sabendo-se que as extremidades B e D são impedidas de girar, para o carregamento dado determinar a máxima tensão
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com G = 77 GPa e τ=150 MPa. Determinar a correspondente tensão de cisalhamento máxima.
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com G = 77 GPa e τ=150 MPa. Determinar o correspondente ângulo de torção.
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com G = 77 GPa e τ=150 MPa. Determinar a intensidade do torque T para que o raio do núcleo elástico seja 12,5 mm.