Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 39
Duas peças de madeira de , de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na junta são, respectivamente de na tração (perpendicular ao chanfro) e de no cisalhamento (paralelo ao chanfro), determinar a maior carga axial P que pode ser aplicada.
Passo 1
Esse caso especial podemos pensar da seguinte maneira. A nossa barra estará sujeita, no estado inicial, apenas a uma tensão na direção X. Se formos analisar dessa maneira as tensões que temos, veremos que:
Fazendo as coordenadas do nosso círculo, teremos que:
Sendo assim teremos que:
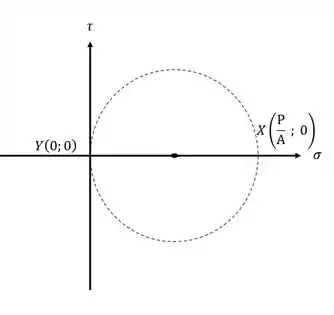
Assim o raio da circunferência será dada por:
E para determinarmos essas tensões no estado girado pelo círculo de mohr, precisamos lembrar do seguinte:
Ou seja, um ângulo que gera uma rotação no sentido horário no estado plano de tensões gera no círculo de mohr o dobro da mesma rotação no sentido anti-horário, e vice versa, com isso já conseguimos pegar o esquema do nosso problema, então vamos ao cálculo.
Passo 2
Vamos girar o nosso ângulo em dobro no sentido anti-horário, como o nosso plano é o de 22°, vamos girar no sentido anti-horário com 44°, sendo assim, teremos que:
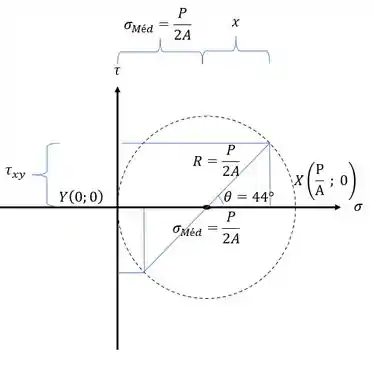
A máxima tensão cisalhante é dada por:
E verificando a tensão x normal teremos que:
E verificando a tensão y normal teremos que:
Para garantirmos que não haverá ruptura da nossa seção, precisamos selecionar a menor carga P encontrada, porque se escolhermos a maior, ela irá romper quem suportaria menos carga, porém, se escolhermos a menor, não oferecerá riscos para a maior, sendo assim, teremos que: