Se o eixo é acionado pelo motor com uma velocidade angular e a aceleração angular no instante mostrado, e a roda de rola sem deslizar, determine a força de atrito e a reação normal sobre a roda, e o momento que tem de ser fornecido pelo motor nesse instante. Suponha que a roda é um disco circular uniforme.
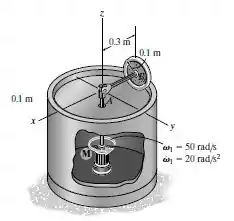
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos que , onde . Logo:
A partir do desenho, podemos fazer a seguinte relação:
Como , temos:
Temos que , onde:
Do enunciado, temos que , portanto:
Então:
As componentes são dadas por:
Agora temos todos os dados necessários para calcular as componentes do momento. Elas são dadas por: