Um eixo de aço de diâmetro de comprimento é fixo em uma extremidade e suporta um propulsor a hélice de massa e momenta de inércia de massa na outra extremidade (Figura 8.27). Determine a frequência natural fundamental de vibração do eixo em:
(a) vibração axial;
(b) vibração torcional;
Dados: , , , .
Bom! E falando agora sobre o canvas pra parte do robô cilíndrico, vou destacar aqui algumas coisas em especial...
Passo 1
E aí, galerinha!
Bom! Bora lá pro que interessa!
Vamos começar fazendo um esboço do nosso eixo, pra entender melhor o que tá acontecendo...
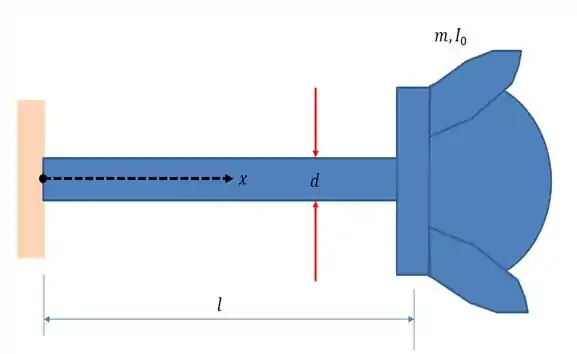
Passo 2
a) Para vibração axial, temos que...
Usando a densidade do aço , temos que a massa vai ser dada pelo produto de pelo volume do eixo, que nada mais é que um cilindro...
Uma vez que a massa total , então temos que...
Bom! De acordo com a tabela , o valor de para é dado por interpolação linear...
Sendo assim, a frequência natural de vibração torcional vai ser dada por...
Uma vez que para o aço, obtemos que...
Passo 3
b) Para vibração torcional, por sua vez, o valor de por sua vez, vai ser...
Onde é o momento polar de inércia. Para o eixo, temos que...
A densidade por sua vez, a gente já sabe que é...
Lembrando qe estamos dividindo por pra fazer o ajuste para . Calculando o momento polar do eixo...
O valor de então, vai ser...
Uma vez que tende a zero, então temos que...
Sendo do aço igual à , temos que...
Resposta
a)
b)