Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 59
Se o eixo AB gira com uma velocidade angular constante , determine as componentes X, Y, Z de reação no mancal radial A e no mancal axial B no instante mostrado. A placa fina tem uma massa de 10 kg. Despreze a massa do eixo AB.
Passo 1
Começaremos o exercício definindo os eixos de rotação xyz com origem no centro de massa da placa conforme o esquema a seguir:
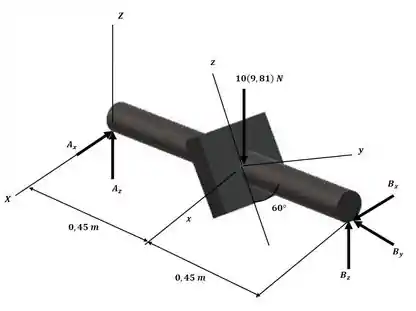
Sendo assim, podemos escrever a velocidade angular da seguinte forma com o auxílio da vista lateral a seguir:
Uma vez que está sempre na direção do eixo –Y e tem uma magnitude constante, . E ainda, como , , então:
Podemos ainda calcular os momentos de inércia do sistema com relação aos eixos definidos:
Passo 2
Agora iremos aplicar o conjunto de equações do movimento 21-25 apresentadas no livro, ainda com base na figura apresentada no passo 1:
Essa será nossa equação 1.
Essa será nossa equação 2.
Passo 3
Agora iremos aplicar os somatórios de força nas direções X, Y e Z.
Essa será nossa equação 3.
Essa será nossa equação 4. Das equações 2 e 3, temos que:
Agora substituindo a equação 4 na equação 1:
E substituindo esse valor na equação 4: