Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 1.Problemas - Ex. 24

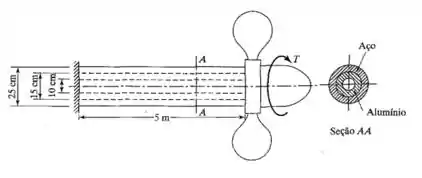
Um eixo de hélice composto fabricado em aço e alumínio é mostrado na Figura 1.72.

  1. Determine a constante torcional do eixo.
  2. Determine a constante torcional do eixo composto quando o diâmetro interno do tubo de alumínio para 5 cm em vez de 10 cm

Passo 1

Saalve, tudo certo? Bora pra questão sem enrolar! Pode parecer bagunça mas vai ficar tranquilo, se liga: O aço e o alumínio pode ser tratado como duas molas torcionais em pararelo. A constante junta dá:

k t = π G 32 l ( D 4 - d 4 )

  1. Para o alumínio: G = 26 10 9 P a , ; l = 5   m , D = 0,15   m , d = 0.1   m :

    2. k t 2 = π 26 10 9 32 5 0,15 4 - 0,10 4 = 0,207 10 6 N - m / r a d

    k e q = k t 1 + k t 2 = 5,34072 10 6 + 0,206 10 6 = 5,5438 10 6 N - m / r a d

    Passo 2

  2. Com G = 26 10 9 P a , l = 5   m , D = 0,15   m e d = 0,05   m

k t 2 = π 26 × 10 9 32 5 0,15 5 - 0,05 4 = 0,255 × 10 6   N - m / r a d

k e q = k t 1 + k t 2 = 5,34072 × 10 6 + 0,255 × 10 6 = 5,5959 × 10 6   N - m / r a d

Resposta

k e q = 5,5959 × 10 6   N - m / r a d

Ver Outros Exercícios desse livro