O eixo maciço tem conicidade linear de em uma extremidade e na outra extremidade. Deduza uma equação que dê a tensão de cisalhamento máxima no eixo em uma localização ao longo da linha central do eixo.
Passo 1
Um eixo no formato de tronco de cone sofre um torque .
Queremos uma expressão para a tensão máxima de cisalhamento em função da posição .
Vamos precisar da fórmula da torção:
Características do eixo:
- Raio maior: .
- Raio menor: .
- Momento polar de inércia em uma seção com raio r: .
- Comprimento do eixo: .
Considere todos esses caras como conhecidos!
Nossa meta é deixar a tensão máxima em função de ! A tensão máxima sempre ocorre na borda do eixo!
Passo 2
Como queremos fazer em função de , vamos deixar cada termo na fórmula em função de !
O torque é constante, então desencana dele!O momento polar de inércia depende do raio da seção transversal, que é a outra letra da fórmula! Então precisamos deixar o raio em função de !
Olha a figura que vai ficar tudo claro. Só escolhe uma distância para uma seção que vai ter raio e dá nome aos bois com o que a gente sabe: e .
Agora é só fazer semelhança de triângulos (ou usa a tangente do ângulo ali).
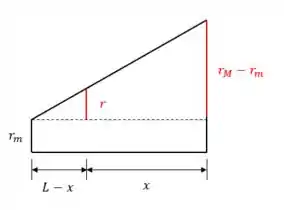
O raio em função de fica como
Passo 3
Agora vamos substituir na fórmula pra tensão!
Resposta
Tensão máxima: