Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 103
O eixo vazado mostrado é feito e um aço doce, que é considerado ser elastoplástico com e . A intensidade dos troques T é lentamente aumentando, até que a zona plástica atinja a superfície interna do eixo, quando então estes são removidos. Determine:
- A intensidade e onde ocorre a máxima tensão residual de cisalhamento.
- O ângulo de torção permanente.
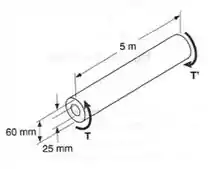
Passo 1
Pelo enunciado temos os seguintes dados apresentados:
Sabemos que a equação do torque é dada por:
Algo importante para sabermos é que como a zona plástica cresceu até chegar na superfície interna do eixo, podemos definir que , com isso podemos escrever a nossa equação da seguinte maneira.
Resolvendo a integral teremos que:
Substituindo teremos que:
Substituindo esses dados na equação, teremos que:
E tendo o valor do torque, podemos determinar o valor das tensões, e assim podemos calcular as tensões relacionadas a cada um dos raios, e separando teremos que:
- (A máxima tensão residual de cisalhamento)
- (A tensão residual de cisalhamento na superfície do eixo)
Passo 2
E agora podemos calcular as tensões residuais, da seguinte maneira:
Como a tensão residual máxima é a maior dentre as duas que calculamos ali em cima, temos que:
Passo 2
Agora para o item B) precisamos determinar o ângulo de deformação. Para isso precisamos fazer uma diferença entre a deformação elástica e máxima, sendo assim teremos que:
Podemos determinar o nosso ângulo de deformação elástica dada pela seguinte equação.
Sabemos que:
Substituindo teremos que:
E assim a nossa deformação angular total é dada pela seguinte equação.
Tendo o torque atuante, podemos determinar a máxima deformação angular de acordo com a nossa estrutura.
E como queremos a deformação angular permanente, podemos fazer a seguinte conta:
Passando para graus teremos que:
Resposta
A máxima tensão residual de cisalhamento
O ângulo de deformação permanente é dado por