Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 116

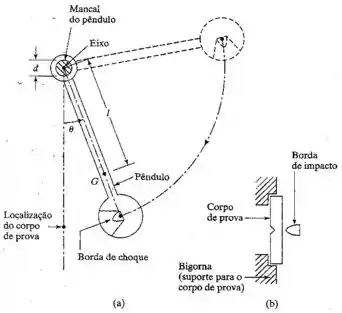
O ensaio de impacto de Charpy é um teste dinâmico no qual um corpo de prova é atingido e quebrado por um pêndulo (ou martelo) e a energia absorvida na quebra do corpo de prova é medida. Os valores de energia servem como um guia útil para comparar a resistência ao impacto de diferentes materiais. Como mostrado na figura 2.98, o pêndulo está suspenso através de um eixo, é solto de determinada posição e cai sobre o corpo de prova provocando sua quebra. Supondo que o pêndulo oscile livremente (sem nenhum corpo de prova), determine:

  1. Uma expressão para a diminuição do ângulo de balanço para cada ciclo provocada por atrito;
  2. A solução para θ t se o pêndulo for solto de um ângulo θ 0 ;
  3. O número de ciclos após o qual o movimento cessa. Considere que a massa do pêndulo seja m e que o coeficiente do atrito entre o eixo e o mancal do pêndulo seja μ .

Passo 1

O enunciado pede que a gente determine

  1. Uma expressão para a diminuição do ângulo de balanço para cada ciclo provocada por atrito;
  2. A solução para θ t se o pêndulo for solto de um ângulo θ 0 ;
  3. O número de ciclos após o qual o movimento cessa. Considere que a massa do pêndulo seja m e que o coeficiente do atrito entre o eixo e o mancal do pêndulo seja μ .

Equação de movimento para oscilação angular de pêndulo é dado por:

J 0   θ ¨ + m g l sin ⁡ θ ± m g   μ d 2 cos ⁡ θ = 0

Para ângulos pequenos,

θ ¨ + m g l J 0 θ + μ d 2 l = 0

Isso mostra que o ângulo de segurança diminui em μ d 2 l em cada quarto de ciclo.

Passo 2

  1. Para movimento da direita para a esquerda:

    2. θ t = A 1 cos ⁡ ω n t + A 2 sin ⁡ ω n t + μ d 2 l

    ω n = m g l J 0

    Seja

    θ t = 0 = θ 0                 e                 θ ˙ t = 0 = 0 .

    A 1 = θ 0 - μ d 2 l ,               A 2 = 0

    θ t = θ 0 - μ d 2 l cos ⁡ ω n t + μ d 2 l

    Para movimento da esquerda para a direita:

    θ t = A 3 cos ⁡ ω n t + A 4 sin ⁡ ω n t + μ d 2 l

    ω n t = π ,                 θ = - θ 0 + 2 μ d 2 l ,                 θ ˙ = 0

    da solução anterior.

    A 3 = θ 0 - 3 μ d 2 l ,                 A 4 = 0

    θ t = θ 0 - 3 μ d 2 l cos ⁡ ω n t - μ d 2 l

    Passo 3

  2. O movimento cessa quando

θ 0 - n 4 μ d 2 l < μ d 2 l

onde n denota o número de ciclos.

Resposta

  1. θ ¨ + m g l J 0 θ + μ d 2 l = 0
  2. θ t = θ 0 - 3 μ d 2 l cos ⁡ ω n t - μ d 2 l
  3. θ 0 - n 4 μ d 2 l < μ d 2 l
Ver Outros Exercícios desse livro