Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 61
A escora de alumínio tem 10mm de espessura e a seção transversal mostrada na figura. Se for submetida a um cisalhamento , determine o fluxo de cisalhamento nos pontos A e B.
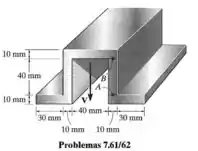
Passo 1
Dados da questão: ,
A questão pede o fluxo de cisalhamento em A e B:
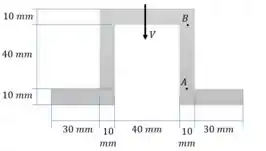
Estratégia de resolução: Começamos calculando o centroide e o momento de inércia. Depois calculamos os momentos estáticos nos pontos de interesse e por fim usamos a equação de fluxo de cisalhamento
Passo 2
Iniciamos encontrando o centroide:
Passo 3
Agora, calculamos o momento de inércia
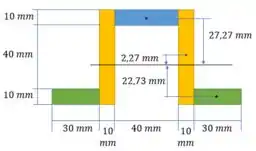
Passo 4
Momento estático em A:
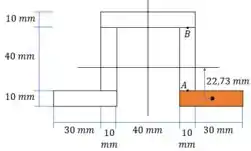
Momento estático em B:
Passo 5
Fluxo de cisalhamento em A:
Fluxo de cisalhamento em B:
Resposta
Exercícios de Livros Relacionados
Resolver o Prob. 5.76, assumindo que a força de 750N é dirigida verticalmente para cima.
Resolver o Prob. 5.74, assumindo que h = 300m m .
Duas forças são aplicadas ao componente de máquinas A B D , como mostrado. Sabendo-se que a seção transversal do componente é retangular com 30x45m m , determinar as tensões, normal e de cisalhamento,
Uma força de 4450N é aplicada no ponto A do membro de ferro fundido mostrado. Sabendo-se que o membro tem um diâmetro de 45m m , determinar as tensões, normal e de cisalhamento, no ponto H .
Três forças são aplicadas à barra mostrada. Determinar as tensões, normal e de cisalhamento, nos três pontos indicados.