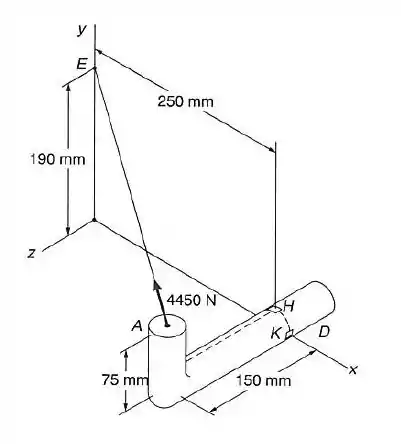
Uma força de é aplicada no ponto do membro de ferro fundido mostrado. Sabendo-se que o membro tem um diâmetro de , determinar as tensões, normal e de cisalhamento, no ponto .
Passo 1
Nesse tipo de questão com esforços combinados, a primeira coisa a fazer é substituirmos essa força por um sistema de forças e momentos equivalentes, aplicados no centróide da seção que passa por e .
Isso vai representar os esforços internos nessa seção, que a gente vai usar para calcular as tensões.
Vamos começar achando as projeções de nos eixos coordenados. Conseguimos projetar ela no eixo e no plano , e depois nos eixos e , pelas relações:
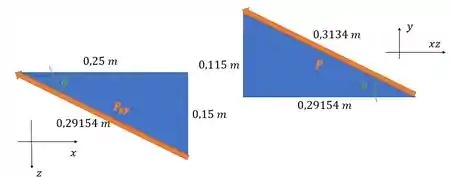
Passo 2
Agora vamos achar os representantes dos esforços internos no centroide da nossa seção . Antes, vamos fazer uma mudança para facilitar nossa vida, e mudar a localização dos nossos eixos coordenados para ajudar nas contas:
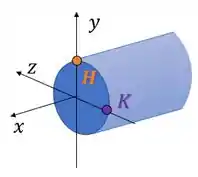
É maneiro, nesses exercícios, deixar o eixo como o eixo paralelo ao eixo da barra. Aí a gente consegue usar as fórmulinhas de tensões com mais tranquilidade.
Temos essas componentes, em relação esse novo sistema de coordenadas:
- Força axial entrando na seção:
- Cortantes:
- Torção:
- Momentos:
Passo 3
Bora calcular as propriedades geométricas da seção transversal:
Passo 4
Agora é aplicar nossas fórmulinhas de tensão para o ponto . A força axial e o momento em geram tensão normal. O momento não vai gerar tensão normal porque está na linha neutra desse esforço. Os dois esforços causam compressão:
Passo 5
E a gente vê que a torção e o cortante geram cisalhamento no mesmo sentido:
Para um semicírculo de raio :
A expessura da seção é: . Aí fica:
Já o cortante não vai gerar cisalhamento porque o nosso ponto está situado na fibra superior da seção.
Então é isso. Achamos tudo! Uhul!
Resposta
(no novo sistema de coordenadas)