Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 77
Resolver o Prob. 5.76, assumindo que a força de é dirigida verticalmente para cima.
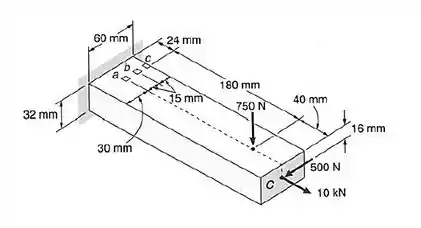
Passo 1
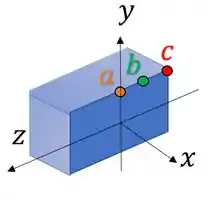
Algo muito importante antes de partir para as continhas, é definir nossos eixos coordenados. É interessante colocar o eixo como normal à nossa seção. Vamos fazer assim:
Nesse tipo de questão com esforços combinados, a primeira coisa a fazer é substituirmos essas forças por um sistema de forças e momentos equivalentes, aplicados no centróide da seção que passa por e .
Isso vai representar os esforços internos nessa seção, que a gente vai usar para calcular as tensões. Temos essas componentes, em relação esse nosso sistema de coordenadas:
- Força axial saindo da seção:
- Cortantes:
- Não temos torção porque todas as forças tem linha de ação passando por .
- Momentos:
Passo 2
Bora calcular as propriedades geométricas da seção transversal:
Passo 3
Agora é aplicar nossas fórmulinhas de tensão para o ponto . A força axial e o momento em geram tensão normal. O momento não vai gerar tensão normal porque está na linha neutra desse esforço. A força axial causa tração e o momento causa compressão.
E a gente vê que o cortante gera cisalhamento:
Para a parte da seção acima do eixo :
A expessura da seção é: . Aí fica:
Já o cortante não vai gerar cisalhamento porque o nosso ponto está situado na fibra inferior da seção, em relação ao cortante.
Passo 4
Vamos para o ponto . A força axial e os momentos geram tensão normal. A força e o momento geram tração, o gera compressão.
E a gente vê que o cortante gera cisalhamento:
Para a parte da seção acima do eixo :
A expessura da seção é: . Aí fica:
Já o cortante não vai gerar cisalhamento porque o nosso ponto está situado na fibra inferior da seção, em relação ao cortante.
Passo 5
Vamos para o ponto . A força axial e os momentos geram tensão normal. A força e o momento geram tração, o gera compressão.
E a gente vê que o cortante não gera cisalhamento, porque esse ponto está na fibra inferior da seção.
Já o cortante não vai gerar cisalhamento também, porque o nosso ponto está situado na fibra inferior da seção, em relação ao cortante.
Resposta
(a)
(b)
(c)