39. Uma esfera de está em repouso sobre superfície parabólica lisa. Determine a força normal que ela exerce sobre a superfície e a massa do bloco necessária para mantê-lo na posição de equilíbrio mostrada na figura.
Passo 1
Para encontrarmos a força norma que a superfície aplica na esfera, vamos considerar o sistema em equilíbrio, assim as seguintes equações devem ser satisfeitas:
Temos que lembrar que a força de tração que a corda faz na esfera é igual a força peso do bloco, já que estão ligados pela mesma corda. Logo:
Lembrando que a esfera exerce uma força peso para baixo que é dada por:
Mas temos um detalhe a ser notado, a força normal ela tem direção perpendicular ao ponto da superfície onde se encontra a esfera, logo teremos que decompor essa força em suas componentes horizontal e vertical, para aí sim usarmos as equações acima.
E como faremos isso? Bem vamos pensar um pouco, a superfície no qual esfera se encontra é parabólica e a figura do enunciado fornece a função que descreve essa parábola.
Então basta lembrar de uma propriedade da deriva que diz que a derivada da função em um certo ponto, nos da a tangente do ângulo de inclinação da reta tangente que passa no ponto, no caso o ângulo que a reta faz com a horizontal.
Essa reta como é tangente ao ponto de interesse, por consequência ela será perpendicular a força normal no mesmo ponto e o ângulo que achamos será o ângulo que a normal faz com eixo , isso é constatado por relação básica de trigonometria, a figura abaixo ilustra a situação.
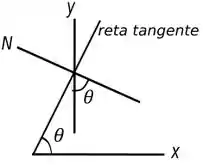
Passo 2
Vamos então derivar a função que descreve a superfície parabólica em relação ao ponto que a esfera encosta na superfície , temos:
Logo:
Passo 3
Agora podemos abrir as equações do passo com tranquilidade.
Então:
Agora para :
Passo 4
Então encontramos as seguintes equações do passo :
Substituindo a primeira na segunda, temos:
Agora que temos , podemos achar a força norma molinho, basta substituir na primeira equação esse resultado, então: