Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 210
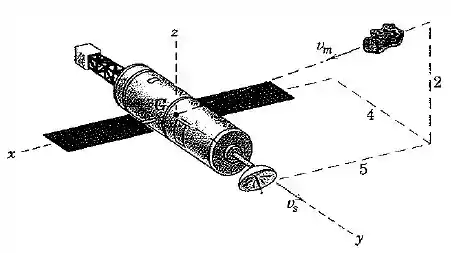
Uma espaçonave de está viajando no espaço profundo com uma velocidade quando um meteoro de se deslocando com uma velocidade de módulo na direção mostrada colide e se prende à espaçonave. Determine a velocidade final do centro de massa da espaçonave. Calcule o ângulo entre e a velocidade inicial da espaçonave.
Passo 1
Pela conservação de momento linear:
Vamos escrever os dois vetores velocidade. Começando pela espaçonave:
A velocidade do metoro é um pouco mais complicada. Vamos começar calculando o vetor unitário na direção mostrada na figura:
E a velocidade do metoro é simplesmente o módulo multiplicado por esse vetor unitário:
Passo 2
E agora é só substituir na nossa equação:
E agora é só resolver essa equação para encontrar :
Passo 3
Agora falta calcular o ângulo entre e a velocidade inicial . Para calcular o ângulo entre dois vetores, é útil lembrar da fórmula para o produto interno:
Começamos então calculando o produto interno:
E então:
E os módulos são:
Agora é só substituir na fórmula:
Resposta
A velocidade final da espaçonave é e o ângulo mede .