Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 70
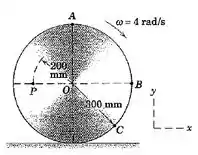
5/70) O disco circular rola sem deslizar com uma velocidade angular no sentido horário . Para o instante representado , escreva as expressões vetoriais para a velocidade de com relação a e para a velocidade de .
Passo 1
Então galera , como visto anteriormente , a velocidade do ponto em relação a é dada por :
Além disso, como indicado no enunciado exposto na figura do enunciado , temos que :
Sendo assim ,
Passo 2
Bom pessoal , utilizando raciocínio análogo ao procedimento anterior , a velocidade de é dada pela relação :
Sendo assim ,
Portanto ,
Resposta
Exercícios de Livros Relacionados
Determine a velocidade angular ω do aríete AE do triturador de pedras na posição em que θ = 60 ° . A manivela OB possui uma taxa de velocidade angular de 60 rpm. Quando B está na parte mais baixa do s
O eixo em O conduz o braço AO a uma velocidade no sentido horário de 90 rpm em torno do mancal fixo em O. Utiliza o método do centro instantâneo de velocidade nula para determinar a velocidade de rota
No projeto desse mecanismo, o movimento ascendente do êmbolo G controla o movimento de uma vara de controle presa em A. O ponto B da haste AH está confinado a se deslocar com o curso deslizante sobre
9. Quando apenas duas engrenagens estão engrenadas, a engrenagem motriz A e a engrenagem movida B girarão sempre em direções opostas. A fim de fazer com que elas girem na mesma direção, uma engrenagem
29. A engrenagem A gira com uma velocidade angular constante ω A = 6 r a d s . Determine a maior velocidade angular da engrenagem B e a velocidade no ponto C.