Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 80

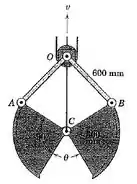
5/80) Os componentes de uma caçamba de mandíbulas simplificada para uma draga são apresentados . O cabo que abre e fecha a caçamba passa através do bloco em O . Com O como um ponto fixo , determine a velocidade angular ω das mandíbulas da caçamba quando θ = 45 ° no momento em que estão se fechando . A velocidade do cabo de controle para cima é de 0,5   m / s quando passa através do bloco .

Passo 1

Então galera , seja β o ângulo A Ô C e B Ô C . Aplicando a lei dos senos ao triângulo indicado na figura , temos que :

0,5 sen ⁡ β = 0,6 sen ⁡ 67,5 °    

Logo ,

  β = sen - 1 ⁡ 0,7699 = 50,3 °

E como a soma dos ângulos internos de um triângulo é 180 ° , temos que :

γ = 90 ° - β = 39,7 °

α = 180 ° - 39,7 ° - 22,5 ° = 117,8 °

Passo 2

Bom pessoal , pelas relações aprendidas nesta seção , sabemos que :

v B = v C + v B / C

Aplicando a lei dos senos ao triângulo da figura , obtemos que :

v B / C sen ⁡ 39,7 ° = v C sen ⁡ 117,8 °

Logo ,

v B / C = 0,361   m / s

Sendo assim , a velocidade angular por sua vez é dada pela relação :

ω = ω B C = 0,361 0,5 = 0,722   r a d / s

Resposta

ω = 0,722   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.93. Se a extremidade A do cilindro hidráulico está se deslocando com uma velocidade V A = 3 m / s , determine a velocidade angular da barra B C no instante mostrado.
No instante mostrado, o caminhão se desloca para a direita de 3m / s , enquanto o tubo rola no sentido anti-horário a ω = 6r a d / s sem deslizar em B. Determine a velocidade do centro G do tubo.
16.91. Se é dada uma velocidade V o = 10m / s ao centro O da engrenagem, determine a velocidade do bloco deslizante B no instante mostrado.
16.96. Se C tem uma velocidade V C = 3 m / s , determine a velocidade angular da roda no instante mostrado.
16.89. Se o segmento C D tem uma velocidade angular ω C D = 6 r a d s , Determine a velocidade do ponto E no segmento B C e a velocidade angular do segmento A B no instante mostrado.