Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 61
Para o estado de tensão mostrado, determine o intervalo de valores de para os quais a tensão normal é igual ou menor que 50 MPa.
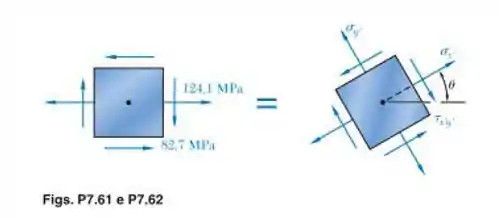
Obs: na verdade os valores para a tensão nesse exercício estão errados, os valores corretos para as tensões são na verdade 90 MPa ao invés de 124,1 MPa e 60 MPa ao invés de 82,7 MPa.
Passo 1
Vamos lá, mais um exercício do nosso querido Beer! Para resolver esse exercício, vamos precisar desenhar o círculo de Mohr para poder analisar os valores possíveis de para a condição dada. E a análise vai ser praticamente toda por trigonometria.
Agora, para desenhar o círculo de Mohr, vamos precisar calcular a tensão média, o raio do círculo e as direções dos planos e tensões principais. Então vamos lá!
Passo 2
Vamos começar escrevendo nossas componentes de tensão que vem do elemento dado no enunciado, onde temos:
Agora, vamos calcular a tensão média, que é dada por:
Agora, vamos calcular o raio do nosso círculo de Mohr, que é dado por:
Beleza! Com esses dados conseguimos esboçar nosso círculo de Mohr, que será dado por:
Passo 3
Beleza! Então, com o círculo de Mohr do passo 2, podemos encontrar as direções principais por trigonometria, onde teremos:
Substituindo os valores conhecidos, chegamos em:
Beleza, temos todas as informações com relação ao nosso círculo para o estado padrão. Agora vamos delimitar no círculo de Mohr a região onde temos a tensão , então teremos:
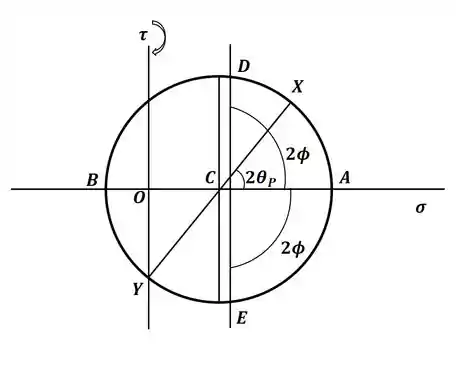
Podemos ver que os valores aceitáveis serão os que estão dentro do arco de circunferência DBE. Agora, vamos encontrar o valor para o ângulo , que pode ser encontrado através da seguinte relação trigonométrica:
Não destacamos no círculo o ângulo do lado em que estamos aplicando a relação trigonométrica por falta de espaço, mas sabemos que quando os ângulos são opostos pelo vértice, eles são iguais, então é justamente isso que fizemos ali. Agora, nós conhecemos o valor de , que é a coordenada do centro do círculo e também o seu raio, então, o valor de será:
Passo 4
Beleza! Agora nós vamos encontrar os ângulos entre os pontos que já temos até os limites do arco para os valores possíveis de , sempre lembrando que uma rotação no elemento diferencial equivale a uma rotação de no círculo de Mohr. Então, começando do ponto X até o ponto D, teremos:
Agora, do ponto X até o ponto E teremos:
Com esses dois valores, nosso intervalo para será:
Feshooow!