Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 80
Para o estado de tensão do Problema 7.69, determine (a) o valor de para o qual a tensão de cisalhamento máxima seja a menor possível e (b) o valor correspondente da tensão de cisalhamento.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, nós vamos precisar encontrar uma expressão para e depois verificar se a tensão de cisalhamento máxima ocorre no plano ou não, para então podermos encontrar o valor de e depois a tensão de cisalhamento correspondente.
Passo 2
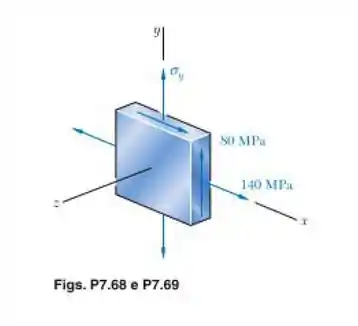
Vamos começar escrevendo as tensões fornecidas no elemento diferencial, que são:
Agora, nós sabemos que a tensão média pode ser encontrada através de:
E que, para o raio do círculo de Mohr, podemos utilizar a seguinte fórmula:
Agora, vamos chamar essa expressão dentro da equação do círculo de Mohr de , onde teremos:
Substituindo essa expressão na equação para a tensão média e para o raio do círculo de Mohr, chegamos nas seguintes equações:
E, sabendo que as tensões nos extremos do círculo, pontos A e B, podem ser dadas por:
Substituindo as expressões para e R, teremos:
Passo 3
Beleza! Agora vamos assumir que a tensão de cisalhamento máxima é a própria tensão no plano, onde nesse caso, temos que a tensão de cisalhamento máxima é igual ao raio do círculo de Mohr, ou seja:
Então, para esse caso, a tensão de cisalhamento será mínima quando tivermos:
Para esse valor de , podemos calcular a tensão média e a tensão na direção através das fórmulas lá do passo 2, então teremos:
E, como nós comentamos no início desse passo, a tensão de cisalhamento será igual ao raio do círculo, então teremos:
Então, podemos calcular as tensões nos pontos A e B, através das fórmulas lá do passo 2, então teremos:
Então, nesse caso, nossa tensão máxima e mínima serão:
E, a tensão de cisalhamento máxima pode ser encontrada através de:
Opa, pera lá! Esse valor é maior do que o valor que assumimos, que seria o raio do círculo, isso quer dizer que nossa suposição está errada, então devemos seguir com a análise.
Passo 4
Beleza! Agora então vamos assumir que a tensão máxima ocorre no ponto A, ou seja:
Substituindo a expressão para , teremos:
E, tendo , a nossa equação para o cisalhamento máximo se torna:
Então, para ter a menor tensão de cisalhamento máxima, vamos derivar a expressão para com relação a (já que nosso u depende de ), para tentar achar um mínimo. Então teremos:
O que também não é possível, já que nossa tensão de cisalhamento não é zero, então não temos mínimo para essa função.
Passo 5
Dessa forma, o valor ótimo de u (ou seja, o valor de para o qual a tensão de cisalhamento máxima é a menor possível) ocorre quando a tensão máxima fora do plano é igual a tensão máxima no plano, ou seja, quando tivermos:
Então, substituindo as expressões para e para o raio do círculo, teremos:
Agora precisamos isolar dessa equação, então vamos lá:
Agora, substituindo os valores conhecidos, chegamos em:
E, com esse valor de u, podemos finalmente encontrar a resposta para a letra (a), pegando a equação para lá do passo 2 e substituindo os valores conhecidos, chegamos em:
Ufa! Esse é o nosso valor de , bora pra letra (b) pra fechar esse exercício logo!
Passo 6
Agora ficou fácil, para a letra (b), basta pegar a equação para o raio do círculo de Mohr lá do passo 2, onde temos:
E, nós sabemos que o raio do círculo vai ser a tensão de cisalhamento máxima, então, substituindo os valores conhecidos, chegamos em:
Prooonto! Agora sim acabamos de vez!!