Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 163
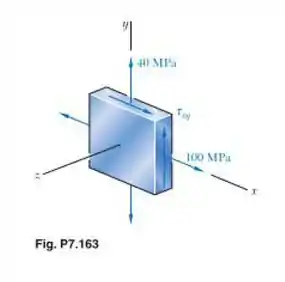
Para o estado de tensão mostrado na figura, determine o valor de para o qual a tensão de cisalhamento máxima é (a) 60 MPa, (b) 78 MPa.
Passo 1
Oiii, e aí, vamos encarar mais um? Esse é meio grandinho, mas vamos lá que a gente consegue! Para resolver esse exercício, vamos utilizar a equação para a tensão de cisalhamento máxima, que é dada por:
No nosso caso, como temos tensões nas direções x e y, e não temos na direção z, então vamos assumir que nossa tensão mínima será a tensão em z, ou seja, será zero (lembrando que depois temos que verificar essa suposição). Então, com isso, conseguimos encontrar o valor da tensão máxima. Com esse valor, podemos encontrar o raio do círculo de Mohr e depois a tensão de cisalhamento pedida no enunciado. Então bora lá!
Passo 2
Beleza! Vamos começar escrevendo as tensões que nós temos no plano, dadas através do elemento diferencial da figura, que serão:
Beleza! Com isso podemos calcular a tensão média, que será dada por:
Agora, para a letra (a), onde temos:
Sabendo que nossa tensão mínima será a tensão em z, ou seja:
Então, da equação para a tensão de cisalhamento máxima descrita no passo 1, teremos:
Isolando a tensão máxima e substituindo os valores conhecidos, temos:
Passo 3
Agora, com o valor da tensão máxima obtida no passo 2, podemos usar a outra fórmula para a tensão máxima, já que ela será uma das tensões principais, e é dada por:
Substituindo os valores conhecidos nessa equação, teremos:
Agora, iremos verificar a nossa suposição de a tensão em z ser a tensão mínima, para isso, calculamos a tensão principal em B, que é dada por:
Então, como temos , será de fato a tensão mínima, então a nossa suposição é válida. Beleza, agora vamos usar a equação para o raio do círculo de Mohr, que é dada por:
Isolando a tensão de cisalhamento dessa equação, teremos:
Substituindo os valores conhecidos, chegamos em:
Belezaaa! Agora é só repetir os cálculos para a tensão de cisalhamento máxima dada para a letra (b), então vamos nessa!
Passo 4
Agora, para a letra (b), com:
Sabendo que nossa tensão mínima será a tensão em z, ou seja:
Então, da equação para a tensão de cisalhamento máxima descrita no passo 1, teremos:
Isolando a tensão máxima e substituindo os valores conhecidos, temos:
Agora, com o valor da tensão máxima obtida no passo 2, podemos usar a outra fórmula para a tensão máxima, já que ela será uma das tensões principais, e é dada por:
Substituindo os valores conhecidos nessa equação, teremos:
Passo 5
Agora, iremos verificar a nossa suposição de a tensão em z ser a tensão mínima, para isso, calculamos a tensão principal em B, que é dada por:
Então, como temos , então a nossa suposição não é válida. Na verdade, então a nossa tensão de cisalhamento máxima será o próprio raio do círculo de Mohr, onde teremos:
Sendo assim, sabendo que a equação para o raio do círculo de Mohr é dada por:
Isolando a tensão de cisalhamento dessa equação, teremos:
Substituindo os valores conhecidos, chegamos em: