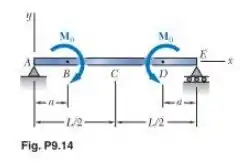
Supondo que a viga A E é um perfil de aço laminado W 360 x 101 e que M 0 = 310k N m ,L = 2,4 m ,a = 0,5 m e E = 200G P a , determine (a) a equação Da linha elástica para a parte B D e (b) a deflexão no ponto C .

E Iy = 1 2 M 0 x 2 - 1 2 M 0 L x + 1 2 M 0 a 2 y c = 3,06m m

Enunciado

Fala aí, galera. Tudo bem? Vamos para mais uma questão.

Primeiramente, devemos determinar a equação do momento em função de que é o eixo que percorre a estrutura. As reações, neste caso, são nulas.

Caso tenha dúvida, aplique o somatório de momento em e depois em

Sabemos que a equação da linha neutra é dada por:

Como dito, precisamos da equação do momento. Além disso, integrando a equação uma vez, temos a rotação e, integrando duas vezes, temos a deflexão.

Agora, temos que encontrar a equação do momento e integrá-la duas vezes. A equação do momento entre e é:

Portanto, integrando duas vezes:

Já entre e :

Portanto, integrando duas vezes:

As constantes serão determinadas pelas condições de contorno. Como a deflexão em é nula, pois trata-se se um apoio:

Já a rotação no centro, onde será nula. Substituindo:

Já onde os dois momentos atuam, a deflexão e a rotação são iguais, logo, substituindo:

Logo, a equação pedida na letra a é:

Portanto, temos a equação da deflexão, bastando substituir os valores para achar a deflexão em Ela será:

Substituindo:

Pronto, mais uma questão feita.