Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 162
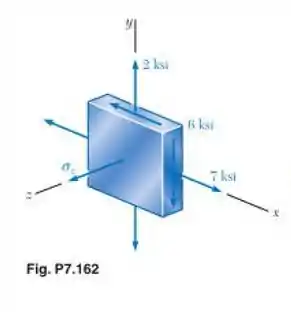
Para o estado de tensões mostrado, determine a tensão de cisalhamento máxima quando (a) , (b) , (c) .
Passo 1
Eaaee galera! Estamos quase acabando o capítulo, falta pouco, bora lá! Para resolver esse exercício, vamos precisar encontrar as tensões principais no plano e depois comparar esses valores com cada um dos valores de dados, para descobrir quais são os valores máximos e mínimos de tensão normal que temos, já que a tensão de cisalhamento máxima é dada por:
Então, para descobrir as tensões principais, sabendo que elas são dadas por:
Vamos precisar da tensão média e do raio do círculo de Mohr no plano xy. Então bora lá!
Passo 2
Beleza! Vamos começar escrevendo as tensões que nós temos no plano, dadas através do elemento diferencial da figura, que serão:
Beleza! Com isso podemos calcular a tensão média, que será dada por:
Agora, o raio do círculo de Mohr será dado por:
Com esses dois valores encontrados, podemos encontrar as tensões principais no plano, dadas por:
Passo 3
Beleza! Agora podemos começar a analisar a letra (a), onde temos:
Então, comparando o valor de com as tensões principais, podemos ver que as tensões máxima e mínima serão:
Então, com isso, nossa tensão de cisalhamento máxima será:
Passo 4
Agora, para a letra (b), vamos repetir a análise feita no passo 3. Agora nós temos:
Então, comparando o valor de com as tensões principais, podemos ver que as tensões máxima e mínima serão:
Então, com isso, nossa tensão de cisalhamento máxima será:
Passo 5
E, pra fechar, para a letra (c), teremos:
Então, comparando o valor de com as tensões principais, podemos ver que as tensões máxima e mínima serão:
Então, com isso, nossa tensão de cisalhamento máxima será:
Shooow! Terminamos mais um exercício, valeeu!