Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 84
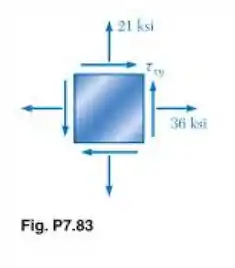
Resolva o Problema 7.83 usando o critério da tensão de cisalhamento máxima.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, nós vamos utilizar a equação da tensão de cisalhamento máxima para descobrir o valor máximo a que o elemento está sujeito e daí comparar com a tensão de escoamento do material, para ver se escoa ou não, e depois calcular o coeficiente de segurança, caso não escoe. Então, sabendo que a tensão de cisalhamento máxima é dada por:
Então, precisamos dos valores das tensões máxima e mínima a que os elementos estão sujeitos, para isso precisamos calcular a tensão média, o raio do círculo.
Passo 2
Vamos começar calculando a tensão média, que é dada por:
Beleza, agora, para o raio do círculo de Mohr, temos a seguinte fórmula:
Substituindo os valores conhecidos, teremos:
Beleza! E nós sabemos que as tensões nos pontos A e B serão dadas por:
Agora sim vamos começar os cálculos.
Passo 3
Beleza! Agora vamos partir para a letra (a), onde temos:
Nesse caso, nosso raio do círculo de Mohr será:
E agora, vamos calcular os valores das tensões nos pontos A e B, onde teremos:
Então, como temos dois valores de mesmo sinal, sabemos que temos um outro círculo de Mohr maior que toca a origem, de modo que teremos:
Agora podemos calcular a tensão de cisalhamento máxima, então teremos:
Como a tensão de cisalhamento máxima é menor do que a tensão de escoamento , então, não terá escoamento. Sendo assim, vamos calcular o fator de segurança, dado por:
Shooow! Fechamos a letra (a). Agora é só repetir os cálculos para as letras (b) e (c), bora lá.
Passo 4
Beleza! Agora vamos partir para a letra (b), onde temos:
Nesse caso, nosso raio do círculo de Mohr será:
E agora, vamos calcular os valores das tensões nos pontos A e B, onde teremos:
Então, como temos dois valores de mesmo sinal, sabemos que temos um outro círculo de Mohr maior que toca a origem, de modo que teremos:
Agora podemos calcular a tensão de cisalhamento máxima, então teremos:
Como a tensão de cisalhamento máxima é maior do que a tensão de escoamento , então haverá escoamento. Opa! Terminamos mais uma, bora pra letra (c) pra fechar de uma vez!
Passo 5
Beleza! Agora vamos partir para a letra (c), onde temos:
Nesse caso, nosso raio do círculo de Mohr será:
E agora, vamos calcular os valores das tensões nos pontos A e B, onde teremos:
Então, como temos dois valores de mesmo sinal, sabemos que temos um outro círculo de Mohr maior que toca a origem, de modo que teremos:
Agora podemos calcular a tensão de cisalhamento máxima, então teremos:
Como a tensão de cisalhamento máxima é maior do que a tensão de escoamento , então haverá escoamento. Fechamos mais um exercício, valeeu!