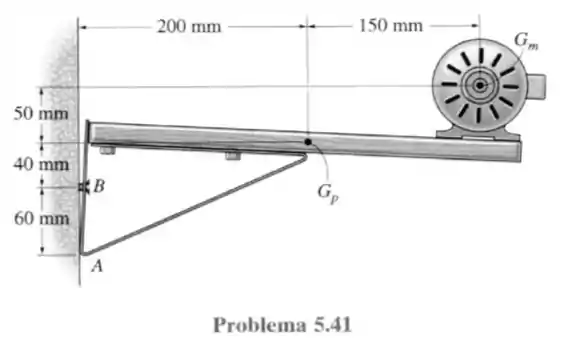
41- A estante sustenta o motor elétrico da figura, que tem massa de e centro de massa em . A plataforma tem massa de e centro de massa em . Supondo que um único parafuso prenda o suporte na parede lisa em , determine a força normal nesse ponto e calcule os componentes horizontal e vertical da reação do parafuso no suporte.
Passo 1
Fala galera do meu Brasil! Tudo de boa ai? Essa questão aí requer um pouco de nossa conhecimento então vamos lá.
Pelo enunciado conseguimos tirar a massa da plataforma, do motor e de três forças que seguram essas outras duas, as forças normais do parafuso e a normal da parede com o suporte, desenhando tudo isso temos o seguinte diagrama de forças:
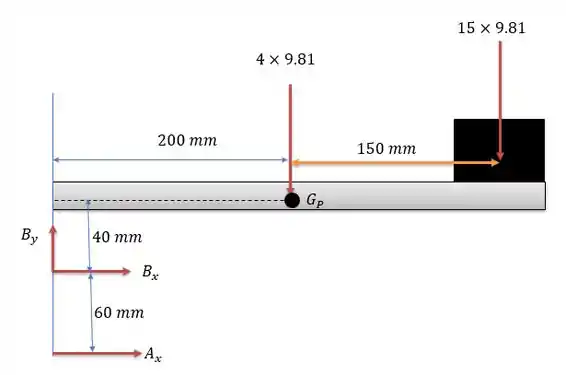
Note que nosso conflito aqui é de resolver a normal na parede em que é e as componentes vertical e horizontal no parafuso em , e para isso que é importante fazermos os desenhos.
A primeira coisa a se fazer é fazer a somatória das forças verticais, já que só existe uma variável que não conhecemos na vertical, fazendo isso nós encontramos:
E fazendo a somatória das forças horizontais ser nula encontramos:
Passo 2
Agora só temos duas variáveis para resolver, e que são a normal da parede e a componente horizontal do parafuso.
E uma outra forma que podemos relacionar essas duas variáveis é fazendo a somatória dos momentos em ser zero (qualquer momento em qualquer outro ponto serve, no caso escolhemos a somatório dos momentos no centro da barra ou em ).
Dessa forma nós temos (para sentido anti-horário sendo o positivo):
Isso nos dará:
Substituindo por teremos (pela equação que encontramos no final do passo 1):
Logo: