54- O tubo liso está em repouso contra a parede nos pontos de contato e . Determine as reações necessárias nesses pontos para suportar a força vertical de . Despreze a espessura do tubo para os cálculos.
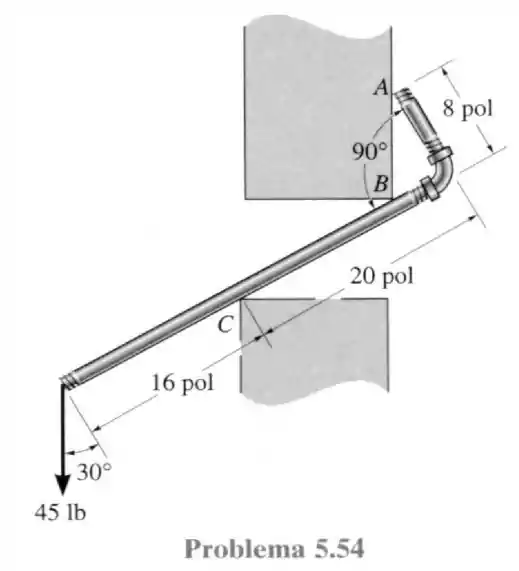
Passo 1
Por estar em contato com quinas o tubo em e em apresenta reações na horizontal e na vertical e em só pode ter reações na horizontal de forma a ficar normal com o tubo. De tal forma que temos o seguinte diagrama de forças.
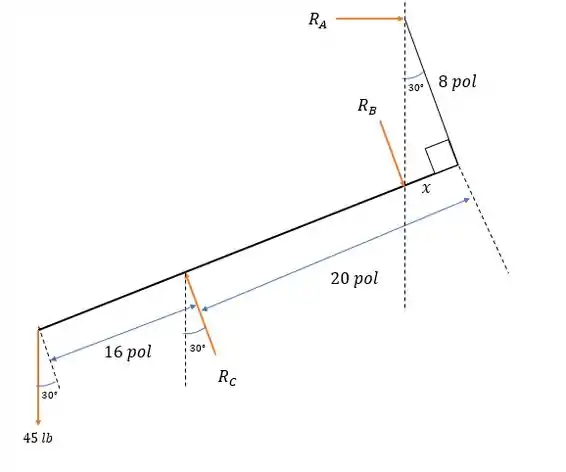
Fazendo a somatória dos momentos em :
Onde a força de gera momento em e .
Onde vale:
Logo:
Passo 2
Agora fazendo a somatória das forças verticais temos:
Somando com a equação encontrada no passo temos:
E
Passo 3
Fazendo a somatória das forças horizontais temos: