Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 14

Expresse a força como um vetor cartesiano

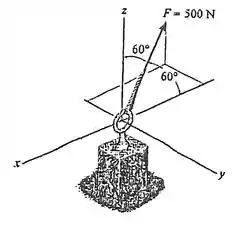
Passo 1

Vamos encontrar as componentes da força nos eixos, para isso usaremos os ângulos de direção e as relações:

cos ⁡ α = F x F

cos ⁡ β = F y F

cos ⁡ γ = F z F

Com eixo x :

cos ⁡ 60 ° = F x 500

F x = 250   N

Com eixo z :

cos ⁡ 60 ° = F z 500

F z = 250   N

Já para o eixo y não temos o ângulo, mas podemos tirar pela relação:

cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ = 1

cos 2 ⁡ 60 ° + cos 2 ⁡ β ° + cos 2 ⁡ 60 = 1

cos 2 ⁡ β = 1 2

β = cos - 1 ⁡ 2 2

β = 45 °

Logo, nossa componente em y :

cos ⁡ 45 ° = F y 500

F y = 354   N

Passo 2

Por fim, escrevendo nossa força como vetor cartesiano:

F = F x i + F y j + F z k

F = - 250 i - 354 j + 250 k N

Resposta

F = - 250 i - 354 j + 250 k N

Ver Outros Exercícios desse livro