Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 8
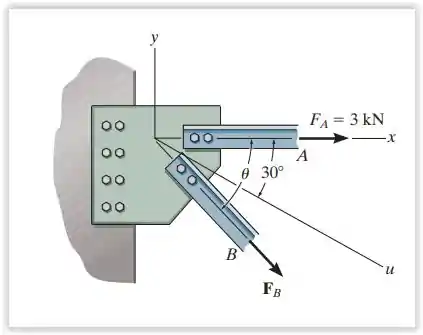
2.8. Se a força resultante precisa atuar ao longo do eixo positivo e ter uma intensidade de , determine a intensidade necessária de e sua direção θ.
Passo 1
Falaaa...
Nessa questão vamos precisar da regra do paralelogramo: para somar dois vetores com a mesma origem traçamos uma linha paralela a cada vetor no finalzinho e o vetor soma vai ser o que encontra o outro lado do paralelogramo formado, assim:
E também vamos precisar lembrar da lei dos cossenos:
Se tivermos um triângulo:
Vale:
Então bora aplicar essas coisas...
Passo 2
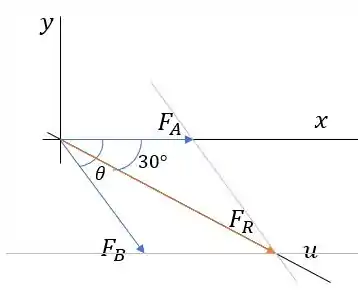
Na nossa questão temos dois vetores e já temos qual é a direção que a força resultante deve ter, que é a direção . Se liga no esqueminha:
Maaaasss pra ser a resultante da soma de e a setinha tem que encontrar o outro lado do paralelogramo que se forma quando traçamos as paralelas, né?
Passo 3
Oh.... Podemos colocar a pontinha do vetor na setinha do vetor e vamos ficar com um triângulo assim:
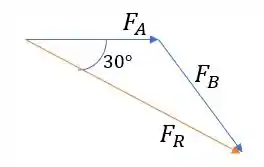
E podemos aplicar a lei dos cossenos:
Substituindo tudo que a gente tem:
Passo 4
Agora “só” falta o ângulo .
Repara que se pegarmos o paralelogramo de novo, temos ângulos iguais que vão nos ajudar:
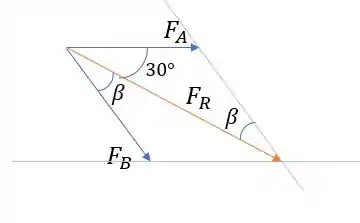
E voltando pro triângulo:
Aplicando a lei dos cossenos de novo, mas no outro ângulo:
Substituindo os valores:
Calmaaa que ainda não acabou...
Pra achar precisamos somar:
Showww... Agora sim acabamos. Bora pra próxima?